Reverberation and absorption
How do we perceive the acoustics in a room? Get an introduction to the concepts of reverberation time and absorption
- The reverberation time is a measure of how fast the sound dies away in a given room.
- The size of the room and the choice of materials determine the reverberation time.
- Once we know the sound absorption coefficient of a material and how much of it there is in a room, we can calculate the total absorption in the room. The unit of measurement is the metric sabin (m2 sabin).
- Once we know the size of the room and the total absorption, using Sabine’s equation we can calculate the reverberation time, even before the room is built.
The following section tells you about the conditions that determine how we perceive the acoustics in a room. The key term here is reverberation time, and the following describes how to measure the reverberation time for a given room. The section also describes how the choice of materials and the ability of the materials to absorb sound strongly influences the reverberation time. In addition, the section introduces Sabine’s reverberation equation. Using this equation, it is possible to calculate the reverberation time in a room, even before it has left the drawing board.
To understand what is meant by good and bad acoustics, it is essential to understand the concept of reverberation time.
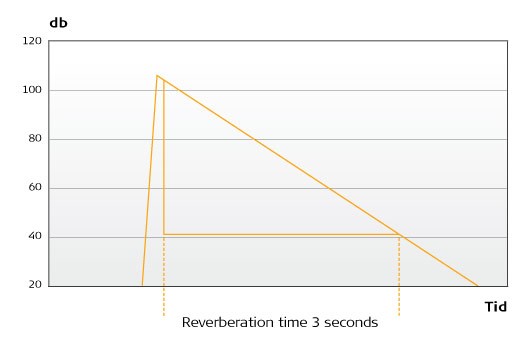
The reverberation time is – in short – a measure of how fast the sound dies away in a room, for example when you clap your hands. Specifically, it is the time (in seconds) it takes for the initial sound pressure level to be reduced by 60 dB. Figure 6 shows the time sequence of the sound pressure level from a handclap in a room with a short reverberation time compared to the time sequence of the sound pressure level from a handclap in a room with a long reverberation time.
Figure 6: Short and long reverberation times
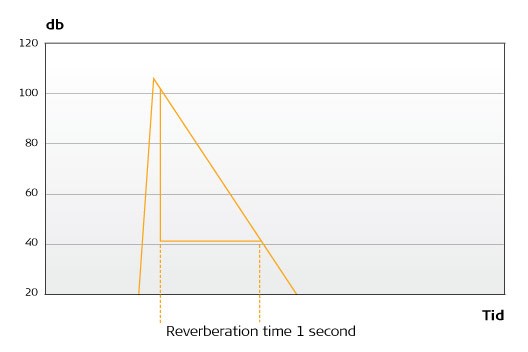
Our ears react to the ‘tail’, and it is the tail which we associate with the room’s acoustics. In the case of a long tail, the room sounds echoey or sonorous. If the tail is short, the room sounds ‘dry’. There are several ways of describing reverberation. A bathroom has a relatively long reverberation and sounds echoey (and is a wonderful place to sing!), but very different to the reverberation in a church, which also sounds echoey. The difference in reverberation is because the two rooms differ greatly in size, but also because in the church there are deep tones that die away, and they are not present in the bathroom. The ear perceives these differences, and connects them to the room’s sound or acoustics. In other words, the individual frequencies die out differently, which is a very important consideration when you want to create good acoustics.
One talks about the frequency dependence of the reverberation time, or reverberation curve, for a given space. And our ears are very sensitive to this. We have mentioned that the size of the room (its volume) has a bearing on the reverberation time. In other words, all else being equal, a large room has a longer reverberation time than a small room. The other important factor which determines the reverberation time of a room is its absorption.
Absorption is a measure of how much sound-absorbing material there is in a room. Some materials have a sound-absorbing effect, even though it might not appear so on the face of it. Thus, plasterboard, glass, and certain wood floors absorb deep sounds. However, we will return to this later. The sound-absorbing effect of different materials varies greatly. Basically, concrete and masonry do not absorb any sound at all. Carpets, textiles, mineral wool and glass wool, cement-bonded wood wool (Troldtekt) etc. on the other hand are very sound-absorbing.
This property is expressed by the sound absorption coefficient (α). The sound absorption coefficient is the ratio between the sound energy which is absorbed by the material (i.e. the non-reflected sound energy) and the sound energy which strikes the material. The absorption coefficient is thus a factor between 0 and 1, where 0 indicates that the material does not absorb any sound energy, while 1 indicates that the material absorbs all the sound energy. Concrete typically has an absorption coefficient of 0.01 -0.02, corresponding to 1-2 per cent. Troldtekt acoustic panels with a mineral wool backing usually have an absorption coefficient of 0.8 -0.9, corresponding to 80-90 per cent.
The sound-absorbing effect of a material in a given room does not, naturally enough, only depend on the size of the sound absorption coefficient, but also on how many square metres of the material there are in the room. So the absorption – or more correctly the equivalent absorption area (A) – is thus the product of the area in square metres multiplied by the absorption coefficient:
A = S × α (m2 sab)
The unit of measurement is the metric sabin (m2 sab), in order not to confuse it with a ‘normal’ area. The absorption expresses the total effect in the room of the material in question. The physical meaning of the absorption can be expressed as the area of an open window (which absorbs 100 per cent, since the sound does not come back into the room) with the same sound-absorbing effect as the actual number of square metres of the material.
If we take, for example, 10 square metres of Troldtekt with a sound absorption coefficient of 0.8: The absorption is 10 × 0.8 or 8 metric sabins. The same effect can be derived from 8 square metres of open windows, which absorb 100 per cent. So acoustically, placing 10 square metres of Troldtekt in the room is the same as having 8 square metres of windows. In the early days of acoustics, the Open Window Unit (OWU) was actually used as a term for absorption, which was indeed pedagogical.
We are now able to set out the most important formula in acoustics, Sabine’s equation, which links the reverberation time (T) with the room’s volume (V) and the absorption (A), and the proportionality factor of 0.16:
T = 0.16 × V/A, where A = S × α
The most important element is that the reverberation time is proportional to the volume of the room (i.e. a room with twice as big a volume has twice as long a reverberation time) and inversely proportional to the absorption (twice as high an absorption gives half the reverberation time). The proportionality factor of 0.16 is a constant which is used to ensure that everything adds up. The reverberation time is, as we know, defined as the time it takes for the sound level to drop by 60 dB. If another definition had been chosen – for example 40 dB instead of 60 dB – the proportionality factor would also have been different.
Sabine’s reverberation equation means that it is possible to calculate in advance the resulting reverberation time when the size (volume) of the room is known, and when you also know how much absorption has been introduced to the room. Even before the room is built, it is therefore possible to predict the reverberation time which will eventually be experienced in the completed room. In order to be able to carry out the calculation as described, in addition to knowing the room’s dimensions, it is also necessary to know the acoustic properties of the building materials which will be used.
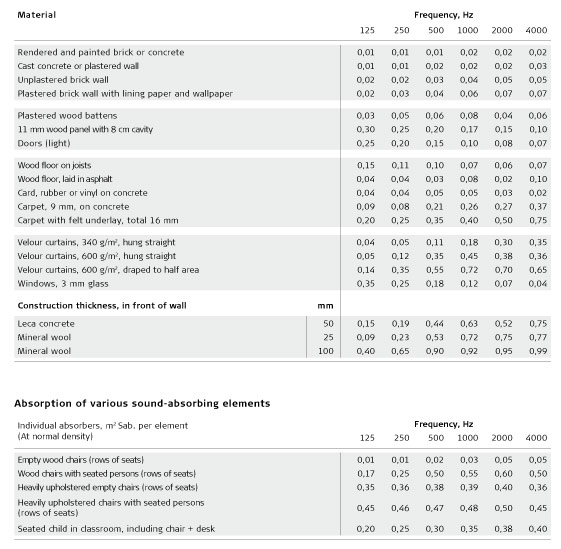
This takes the form of data for the sound absorption coefficient (α) (see, for example, the table on page 9). As the sound-absorbing effect of the materials is frequency-dependent, this is reflected in the α values with the different frequencies, normally in the frequency range 125-4,000 Hz.
It is usually possible to obtain the α values for the various materials from the websites of the individual manufacturers (see www.troldtekt.com, for example). In manuals, and also on the internet, it is possible to find data for building materials which are not specifically acoustics materials, such as floors, windows, masonry and so on. The table on the next page can also be used as a starting point. As can be seen, the calculation is linear; in other words, the contribution made by the different materials and building elements to the absorption are added up to give us the total absorption (A), which is included in Sabine’s equation. For a given room, the calculation is made individually for each frequency band. This gives us the reverberation time in the room for each frequency band, and thus the reverberation curve for the room. The reverberation curve is the reverberation time’s frequency dependence for the room in question. The shape of the reverberation curve expresses the acoustic quality of the room in question. However, we will return to this later.
Figure 7: